Copyright © 1999-2011 by Harold Melton KV5R. All Rights Reserved.
Understanding Shortwave Antennas: Page 5
Basic Radio Theory
|
Wavelength (feet) = 984 ÷ frequency (in megahertz).Example: Middle of FM-band, 98 megahertz,984 ÷ 98 = 10.04 feet.Example: Bottom of AM-band, 0.55 megahertz,984 ÷ 0.55 = 1,789 feet.No, radio waves don’t really go “squiggling”through the air like a wave - we just draw themthat way on x-y (amplititude-time) graphs.
Section of wire, with electron concentrationalternately compressed and expanded.They are “jiggling” back and forth,
|
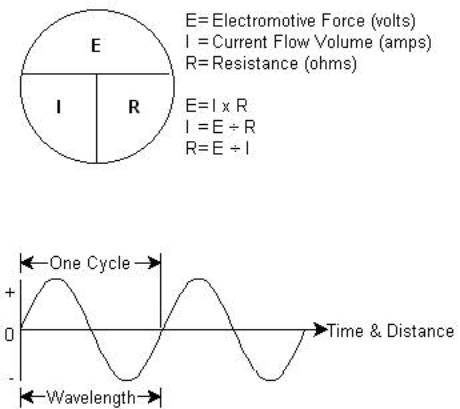
Let’s start here. Electricity, when flowing continuously in one direction is called direct current (DC). DC obeys the same rules as water in a pipe - flow is a function of pressure and resistance. More pressure and less resistance equals more flow. Congratulations - you just learned Ohm’s Law.
Electricity, unlike water, can change its direction of flow very rapidly. Electricity that flows back and forth is called alternating current (AC). Utility power changes directions 120 times per second, AM-band radio about 2 million, FM-band radio about 200 million, and a microwave oven about 4 billion. Two changes, one forward and then one backward, are called one cycle or one Hertz. The number of cycles per second is called the frequency. The distance one cycle travels is called the wavelength, usually measured in meters. Since the speed is fixed (the speed of light), higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths.
Electricity travels down a wire at near the speed of light. At high frequencies, it becomes practical to push electrons into one end of a wire then yank them back out again before the effect reaches the other end. The result of this is that, at such high frequencies, we don’t need a closed loop to have a useful circuit - we can set up an electron oscillation in an open-ended conductor, much like a vibrating coil spring.
If the length of the conductor is 1/2, 3/2, or other odd-multiple half-wavelengths long, the conductor is said to be resonant. The length of the wire is in agreement with the length of the wave, at this frequency.
When electricity flows, it creates a magnetic field. If the direction of the electricity alternates, the polarity of the magnetic field does, too. It also creates an electrostatic field. A radio wave is energy which is alternating between a magnetic field and an electrostatic field. This effect can go on indefinately, while there is a source of energy to sustain it. The energy at a given point diminishes with distance, because the size of the field is growing (and diffusing) as it goes outward.
When a conductor is resonant, it will convert virtually all of the electrical power into radio waves, and thus, is an efficient antenna. (Some power is lost to resistance, but never mind.)
There is a reciprocal law about antennas - any antenna which transmits well can also receive well. When receiving, a radio wave passes across the antenna, inducing an alternating electrical current in it. Variations in the frequency and/or amplititude are called “modulation.” A radio receiver then makes the modulation intelligible (hopefully).
Not all antennas are resonant. A long piece of wire, for example, will pick up a little of just about everything, and induce enough current to drive a receiver. Transmitting antennas, however, are almost always designed to be resonant on the particular frequency of the transmitter.
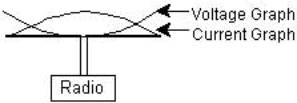
In antenna books, the antenna itself is frequently used as the x-axis of the graph. This antenna is called a half-wave dipole - it has two poles, and is one-half wave long at its design frequency. The sine graphs for voltage and current are shown sitting atop the antenna.
Continued…