manipulating light to see tiny objects
© 2014 by KV5R. Rev. June 1, 2014.
Light Microscope Optics
The “light microscope” is so-called because it images microscopic objects with ordinary visible light. It has a basic limitation: The wavelength of visible light ranges from about 0.4–0.7μm (400–700nm), so the light microscope is limited to things above about 1μm in size—and since that’s just a couple of light-waves, anything 1μm will be just a dot with no detail, no matter how much you magnify it. The wavelength of light, therefore, is the practical limit of optical resolution. The absolute limit, called the “diffraction limit,” is about 200nm, which is about ½-wave of violet light. Anything smaller than that simply cannot affect visible light in any detectable way.
The maximum theoretical optical magnification has long since been known to be about 1200x. But you might say, “I see microscopes advertised with 2,000 or even 2,500 magnification!” Advertizing baloney—they offer a model with a 100x objective and a 20x eyepiece, and call it a 2,000x microscope. The reality is that 2,000 is just bigger (zoomed), with no more detail than 1,000x. Just like zooming a digital picture, it gets bigger with no more resolution. Even 1,000x viewing requires an oil-immersion objective lens, since refraction effects will ruin the image if the light transitions from glass to air and back to glass.
So how do we see beautifully detailed pictures of nano-stuff like bacteria, viruses, and the DNA helix? We must use something much “smaller” than light as the imaging medium, such as a stream of electrons. Thus, the very expensive electron microscope, which is far beyond most hobbyists’ budgets. But thanks to the web, we can see many images made by electron microscopes, and thereby benefit somewhat from their use.
Magnification and Resolution
This is the first thing to understand about microscope optics. Magnification is the main specification you see in microscope advertising, because they know that people look for it, but don’t really understand what it means. A 2000x microscope must be twice as good as a 1000x, right? Not so fast! As described above, light waves can only resolve detail down to a certain size, about 1 micrometer, so around 1000x is where magnification runs into resolution. It’s the same general idea as with digital cameras, where we may have 20x zoom, but if we want more resolution, we’ll need a camera with more pixels, not more zoom, since 1 pixel (picture element) is the basic unit of resolution. With light optics, the wavelength of light is our “pixel.”
So, What Does “Magnification” Mean?
Magnification is the ability of refractive lenses to make things appear larger than they are. They do this by taking a small field of view and expanding it into a larger image that fills the eye (or digital imager). Higher magnification requires a smaller lens and a shorter focal point.
The maximum magnification specification (in microscope ads and specs) is the “total magnification,” which only tells you what lenses are included. For example,
- a “400x” microscope will have 4x, 10x, and 40x objective lenses and a 10x eyepiece lens.
- a “800x” microscope will have 4x, 10x, and 40x objectives and 10x and 20x eyepieces.
- a “1000x” microscope will also have a 100x objective, which is an oil-immersion lens that you’ll almost never use.
- a “2000x” microscope will also have a 20x eyepiece (typically worth about $30). Not really useful at 2000x, but it will give you 80x, 200x, and 800x when combined with the 4x, 10x, and 40x objectives. Thus, when you see a “2000x” microscope, you know that it has 4 objectives and 2 eyepieces (or 2 sets, if binocular).
So, when shopping, one should look beyond maximum total magnification, and attempt to determine exactly what kind of lenses are provided—what is their quality, and what optical aberrations are corrected—as well as the other specifications and features of the microscopes under consideration and comparison.
Magnification and Digital Imagers
What about the magnification when using a digital imager and a big computer screen? It isn’t really important, but if curious, use the formula:
- Screen magnification = (computer-screen-diagonal ÷ imager-chip-diagonal) × adapter-magnification × objective-magnification
- Example: Given a 19″ computer display, a 1/3″ imager chip, and a 0.5x adapter, Ms = (482mm ÷ 6mm) = 80.3 (imager-to-display magnification) × 0.5 (adapter-magnification) × 100x (objective-magnification) = 4016x. Yes, that’s 4x larger than one would see in a 10x eyepiece, but remember, with no more resolution.
- Note that image sensors use “inch” designations that are inflated about 1.5x, being based on the diameters of the old vidicon tubes. For example, a 1/3″ sensor is really about 0.236″ (6mm) diagonal, not 0.333″ (8.5mm) as one might expect.
- The best way to determine it is with a microscope calibration slide
. They are usually about $10, and are precision etched glass slides having 1mm with 100 divisions, so that each division is 10μm. You can also use an inexpensive ($20) hemacytometer
, which has a 3x3mm grid with various subdivisions. Simply place the slide on the stage, select each objective, and measure the divisions on-screen with a metric ruler, then divide the two. You’ll need such factors for each objective to put in your microscope viewing/measuring software that comes with the digital imager
, if you want the software to do on-screen dimensions converted to actual micrometers of the measured specimen. Microscopic measurements of specimens is often important for identification and, when sharing photomicrography, placing a little scale on the picture is simpler and more meaningful than a caption describing the whole optical setup.
Okay, so What Does “Resolution” Mean?
Resolution is the ability to resolve, or differentiate, two close objects, or the fine details of an object; the maximum possible “sharpness” of the image.
You almost never see this as a specification of light microscopes, because it is assumed that you know that the practical resolution of light optics is about 1 micrometer. Objects that are ≈1μm will appear as dots, with no discernible detail, no matter how much you magnify them. To see things and details well below 1μm you must use something else that has a much finer “grain” than light, such as an electron beam.
For light microscopes, magnification runs into resolution at about 1000–1200x. Magnification beyond the limit of resolution is called “empty magnification,” because it’s larger but contains no additional detail.
Microcopists will consider resolution when adjusting the Abbe condenser and its iris. Proper condenser settings must be determined for each objective lens (and specimen) in order to obtain the maximum resolution of which the optics are capable. Such adjustments are made by sight, and become easier with experience.
Numerical Aperature (NA)
Objective lenses are marked with an N.A. number. This refers to the maximum angle of a cone of light that the lens can receive, factored with the lowest refractive index in the optical system. NA = n sinΘ, where n = the refractive index (air=1, water=1.33, glass≈1.52), and Θ (Theta) = ½-angle of the light cone (in degrees). A lens in air cannot have an NA > 1. A 100x lens with an NA of 1.25 must be immersed in a special oil that has a refractive index the same as glass, if it is to work at NA > 1 and realize its best resolution.
The iris (a variable aperture) on the bottom of the condenser controls the actual angle of the light cone reaching the objective, regardless of the NA number on the objective. A cone angle that is larger than the lens NA will result in internal reflections, poor contrast, and poor resolution; while a cone that is much smaller than the lens will result in diffraction interference rings and other optical anomalies in the image. Maximum resolution typically occurs when the iris is open to about 80–90% of the lens’s NA, and the condenser is properly focused on the sample. This initial setting is determined by removing the eyepiece and looking down the tube, setting the iris open to about 80% of the diameter of the objective’s rear aperature, and focusing the condenser so that the edges of the iris appear sharp.
Optical Aberrations
Light is a mixture of many wavelengths (colors), and they do not all refract (bend) the same angle when passing from one transparent material to another with different refractive indices (refraction dispersion), or when passing around the edges of objects (diffraction). This is why we can find light microscopes ranging from $100–$10,000. Most of that cost is in the optics, and more expensive optics provide more corrections for light aberrations, just as with lens systems used in cameras and telescopes. A 40x objective may cost $30, $60, $100, $600, or even $6,000 depending on just how accurately it corrects these optical aberrations.
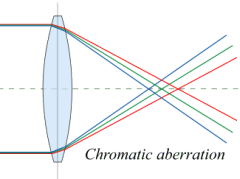
The colors don’t focus
in the same plane.
The most common optical aberration is called chromatic aberration, caused by refraction dispersion. This is where you see fringes of color around objects, because the refraction angle is different for different colors. Thus, red and blue light produce images of slightly different sizes. It is easily seen in a single-element convex lens such as a magnifying glass. It is partly corrected in the achromatic lens system, and almost completely corrected in the (very expensive) apochromatic (APO) lenses. For technical details, see the Wikipedia entries on achromat and apochromat.
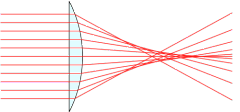
A simple lens doesn’t
create a flat focal plane.
The next optical problem to be corrected is called spherical aberration. This is the property of focal plane “flatness,” and is caused by lenses that do not correct the focal point of all the light coming from all points of the lens, from center to edge. What you see with a typical inexpensive achromatic lens with no spherical correction is the center is in focus, but the focus slightly degrades as you move out toward the edge. This is because a spherical lens will produce a spherical image in the focal plane, not a flat one. Spherical aberration is partially corrected in the “semi-plan” (SP) lens, and fully corrected in the “plan” (PL) lens. In microscope objectives, a regular achromat has a flat field for ≈67% of its diameter; a semi-plan lens has a flat field for about 80% of the diameter, and a plan lens has a flat field for 90–100% of the diameter. Though not needed for casual viewing, plan objectives are particularly desirable for photomicrography, where we want the photo to be in focus from edge to edge. They tend to cost about 50% more than non-plan achromats. Of course, we can take good pictures with non-plan achromats by centering the specimen and then cropping the photo to 60% of it’s original size, but then we will be throwing away some of the resolution by using only the central area of the lens.
The very best lenses (lab-grade) correct both chromatic and spherical errors to a high degree. These are called “aplanatic-apochromatic,” or simply “plan-apo” lenses, usually marked PL/APO. They are very expensive, generally ranging from about $600–$6,000 each. These are used in professional lab-grade microscopes, but actually, can be screwed into any microscope that uses DIN-standard mounting threads. Few amateur microscopists would find any real need to for such expensive optics, but if one comes across a nice set in doctor’s estate sale, they might be irresistible…!
Inexpensive lens systems may also display other aberrations such as flares, internal reflections, and even tiny bubbles in lens coatings. Thus, not all objectives, even of the same price and type, are created equal. Lenses that display such manufacturing defects should be exchanged under warranty. One can tell by closing the iris then loosening and rotating the lens to see if the suspect flaws rotate with it. If they don’t, try rotating the eyepiece or camera adapter, the condenser, and the prism head to determine where such defects are located. If a careful cleaning doesn’t remove the spots, they may well be imperfections in the optical coatings.
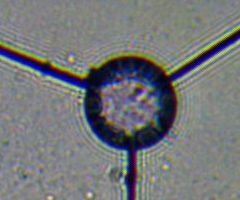
This poor image shows both
diffraction rings and
chromatic aberration.
Diffraction interference patterns appear around objects because light is bent slightly when it passes very small edges, and these slightly bent rays interfere with other rays, producing interference patterns. The darker part of the pattern is where the waves of the crossing rays are out of phase and cancel out. The lighter part of the pattern is where crossing waves are in phase, adding their amplitudes together. In the image, we can see 3 or 4 interference patterns around the dendritic cell. This is not a lens aberration, but operator error—the condenser iris was closed to a small point, making the interference patterns visible. Note that such patterns are always there, but opening the condenser iris to the proper size floods the image from a much wider angle, thus obscuring the interference patterns.
Next, we’ll consider microscope parts and controls.
—KV5R
